NPHS 1530: Analytics

Reliability

n of N Parallel Component Reliability Rn/N Frequently, parallel systems are built where each component has the capability of carrying only part of the system load.   In this case, several of the components must be operating for the system to function.  Power supplies are good examples of this. Power supplies are typically expensive, and their cost increases exponentially with the power required. It is more economical to build multiple parallel power supplies whose individual power outputs are less than the required power for the system they are supplying. For example a power supply subsystem might be constructed of five power supplies, each of which has the capacity to supply forty percent of the system's power. Thus only three or more of the supplies need to be operating for the system to operate at full capacity. The preceding analysis for parallel component systems really calculated the reliability for all systems where only one or more of the N components must be operating (R1/N).   For the two component case shown in Figure 8.5 we can also see that the reliability of the system if both of the components must operate (2 of 2) is: R2/2 = ra * rb Let us develop a formula for systems where n (or more) of N components must be operating by reexamining a three component system. Three Parallel Component System States.          Component  System a b c  Probability   State  Working Working Working ra*rb*rc Operating Working Working Failed ra*rb*(1-rc) Not Operating Working Failed Working ra*(1-rb)*rc  Not Operating  Working Failed Failed ra*(1-rb)*(1-rc) Not Operating Failed Working Working (1-ra)*rb*rc Not Operating Failed Working Failed (1-ra)*rb*(1-rc) Not Operating Failed Failed Working (1-ra)*(1-rb)*rc Not Operating Failed Failed Failed  (1-ra)*(1-rb)*(1-rc)  Not Operating Note that the probability of all three of the components operating, and hence the reliability for three of three operating is: R3/3 = ra * rb * rc We can demonstrate that, for an n=N of N parallel system, the reliability is: Rn=N/N =  Σ i ri This reliability is exactly the same as the series reliability formula because we have added the extra requirement to the general parallel system that all of the components must be operating. The analysis for the general n of N reliability is a little more complex. Referring to the table below, we see that if we wish to calculate the reliability of the 3 component parallel system if 2 or more of the components are operating, that reliability must contain the states where 2 or 3 of the components are operating.

R2/3 = ra * rb * rc +   (3 operate)   ra * rb * ( 1 - rc ) + ra * ( 1 - rb ) * rc + ( 1 - ra ) * rb * rc   (2 operate)

The system reliability (R1/3) where 1 or more of the three components must operate is:

R1/3 = ra * rb * rc +   (3 operate)   ra * rb * ( 1 - rc ) + ra * ( 1 - rb ) * rc + ( 1 - ra ) * rb * rc +   (2 operate)   ra * ( 1 - rb ) * ( 1 - rc ) + ( 1 - ra ) * rb * ( 1 - rc) + ( 1 - ra ) * ( 1 - rb ) * rc   (1 operates)

If we assume all of the component reliabilities are equal ( ra = rb = . . . . . = r), R2/3 and R1/3 become: R2/3 = r3 + 3 *  r2 * ( 1 - r ) R1/3 = r3 + 3 * r2 * ( 1 - r ) + 3 * r * ( 1 - r )2 Recognizing that these are equivalent to a multiple selection binomial probability system, we can simplify and generalize the n of N reliability formula to: Rn/N = ΣNnCnNri(1-r)N-i Where CiK is the number of combinations in K components taken i at a time or: CiK = K!/(i! (K-i)!)        for 0 <= i <= K Suppose a system has six parallel components, each with a reliability of .95.  Four or more of the components must be operating for the system to function.   The reliability of this system would be:

R4/6 =  C46 * ( .95 )4 * ( .05 )2 + C56 * ( .95 )5 * ( .05 ) + C66 * ( .95 )6 * ( .05 )0   15 * ( .95 )4 * ( .05 )2 + 6 * ( .95 )5 * ( .05 ) + 1 * ( .95 )6 * ( .05 )0   .030544 + .232134 + .735092   .99777 The table below gives the system reliabilities for an n of N system (N <= 10) whose component reliabilities are .9.

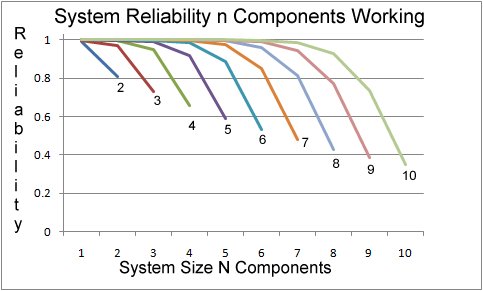
n of N System Reliabilities (r = .9) Operating Components (n) System Parallel Components (N)   2 3 4 5 6 7 8 9 10 1 .99 .999 .9999 1 1 1 1 1 1 2 .81 .972 .9963 .9985 .9999 1 1 1 1 3   .729 .9477 .9904 .9987 .9998 1 1 1 4     .6561 .9175 .9842 .9973 .9996 .9999 1 5       .5905 .8857 .9743 .9950 .9991 .9998 6         .5314 .8503 .9619 .9917 .9984 7           .4783 .8131 .9470 .9872 8             .4305 .7748 .9298 9               .3874 .7361 10                 .3486

:

The graph below shows that the N of N Parallel system is fairly immune to failures, but, as the number of failures approaches the number of system components, the reliability drops off dramatically.

:

:

NOFNREL Spreadsheet The accompanying spreadsheet nofNReliability.xls will also calculate system reliabilities of n of N systems.

:

n of N Reliability Component Reliability  .95 Components Operating Probability n Working n of N Reliability 0 0 1 1 0 1 2 .000002 1 3 .000015 .999998 4 .000356 .999983 5 .005416 .999627 6 .051456 .994211 7 .279335 .942755 8 .663420 .663420

Copyright © 2011 - 2014 Ken Sochats