NPHS 1530: Analytics
Reliability
                 
               
  Parallel System Reliability

The figure below shows a simple system with two parallel components.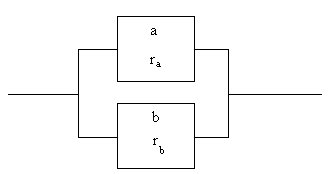

Two Component Parallel System
Following the same method of component analysis as before, we produce the probability outcome tree shown in the table below.

System Component States and System States

abProbability State
 Working  Working ra * rb Operating
WorkingFailed ra * (1- rb) Operating
FailedWorking ( 1 - ra) * rb Operating
FailedFailed  ( 1 - ra) * (1 - rb)   Not Operating 


In a purely parallel system, the system operates if any one of the parallel components is operating. The system is down only if all of the components have failed.  This, of course, assumes that:
  1. the components perform the identical function.
  2. each component has the capacity to carry the full load of the system (i.e. they are fully redundant).
In a later section, we will develop the reliability of a system where more than one of the parallel components must be operating for the system to function. As can be seen from the table above, the reliability of the two component parallel system is:

R = ra * rb + ra * ( 1 - rb ) + ( 1 - ra ) * rb


or, calculating the failure probability:

F = ( 1 - ra ) * ( 1 - rb )

and using the complement formula (4):

R = 1 - F = 1 - ( 1 - ra ) * ( 1 - rb )


If we extrapolate this finding to multiple parallel component systems as we did for series systems, we get:

R = 1 - Π i ( 1 - ri)


For equal component reliabilities (r) we get:

R = 1 - ( 1 - r )n


An example two component parallel system is shown in the figure below. One component has a reliability of .9 and the other component has a reliability of .8. The system reliability is:

R = 1 - ( 1 - ra ) * ( 1 - rb )

R = 1 - ( 1 - .9 ) * ( 1 - .8 )

R = 1 - .1 * .2

R = .98

An Example Two Component Parallel System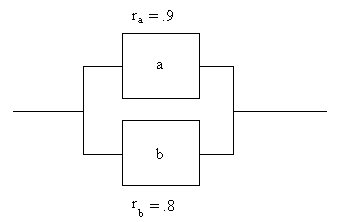
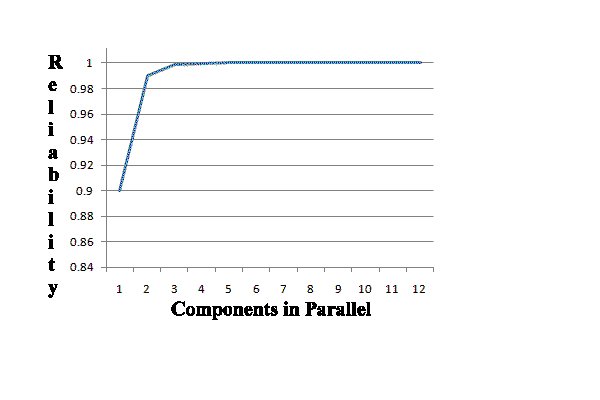
Using the formulae developed we can derive two heuristics for purely parallel systems:
  1. Adding parallel components to a system increases the reliability of the system, often referred to as redundancy.

    R >> 1 - Σ i * ( 1 - ri ) * ( 1 - rnew )


  2. The reliability of a purely parallel system is greater than the reliability of the system's most reliable component.

    R >> rmax
The table and chart below demonstrate how the addition of components in parallel increases the system reliability.
 
Parallel
 Components 		System
 Reliability 
1 0.9
2 0.99
3 0.999
4 0.9999
5 0.99999
6 0.999999
7 0.9999999
8 0.99999999
9 0.999999999
10 1
11 1
121
 Exercise:     The attached spreadsheet has two worksheets. The first shows a general parallel reliability calculation. The second calculates the reliability of a system with n identical components. Alter the reliabilities of the component to explore the effects of component reliability on system Reliability.
 
As we will show later, these heuristics are very helpful to the emergency manager in the early planning stages of a design.  It is often important for a designer to assess a general level of reliability for a system or portion thereof on a relatively quick basis.  In addition, these heuristics will give the designer a "feel" for how the design and design alternatives will behave without having to resort to complex and laborious calculations.
 
Aircraft Engines Example - Parallel
 
Developments in aircraft engine power. economy, and reliability have allowed apirplanes to be built with fewer engines. Early large passenger airplanes were built with four engines. More modern airplanes are built with two engines. In order for this to be accomplished, the reliability of a two engine configuration must be equal to a four engine system
     R2 == R4

where

     R2 = 1-(1-r2)(1-r2)

and

     R4 = 1-(1-r4)(1-r4)(1-r4)(1-r4)

For example, if r4 = .9 R4 = .9999

For R2 = .9999 r2=.99
 
Covid-19 Example - Parallel
 
As measures against Covid-19 the CDC recommends that the public get a vaccine shot(s), wear a mask and practice social distancing.
 
This means that the effectiveness of these measures act in parallel and the reliability can be expressed as:

     RC19 = 1 - (1 - rVac)(1 - rMask)(1 - rSocial)
Current Vaccine effectiveness data: Covid-19 effect

Historical Vaccine effectiveness data: Flu vaccine effectiveness
Example
Continuity of operations is important for many organizations. It is especially important for critical infrastructure businesses and government operations. During an emergency, the maintenance of all the emergency support functions (ESFs) is essential. Many organizations develop continuity of operations plans (COOP) so that the organization can continue to operate during and survive the consequences of a disaster.

 Definition     Continuity of Operations (COOP) Plan: Procedures to ensure the continued performance of core capabilities and/or critical government operations during any potential incident.

Source:FEMA Strategic Plan Fiscal Years 2008 – 2013
 
We can view aspects of the continuity problem using reliability principles.

A company has identified the role of a database administrator (DBA) as crucial to the functioning of the buiness. The DBA guarantees the function and credibility of all data operations for the company.

Each DBA is essentialy a service module with a reliability. For this analysis we will assume each DBA works a single shift per day with no overtime. We can estimate a reliability for the DBA from work characteristics: vacation, business travel, holidays, sick days, etc. Suppose that a DBA is unavailable for work for 67 days per year. He or she is thus annually available for work for 298 days. In other words we could estimate the DBA's reliability as 298/365 = .816.
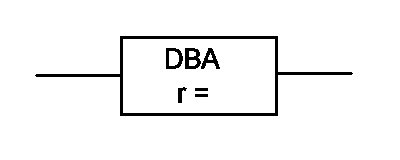The table below shows the calculated system reliability for various numbers of DBAs.
 
Component Reliability = 0.816
 
Number of
 Components 		System
 Reliability 
1 0.816
2 0.9661
3 0.993770496
4 0.998853771
5 0.999789094
6 0.999961193
7 0.99999286
8 0.999998686
9 0.999999758
10 0.999999956
 
The attached spreadsheet contains the DBA model.
 
 Exercise:    
 
              
Copyright © 2011 - 2022 Ken Sochats