and

NPHS 1530: Analytics

Reliability

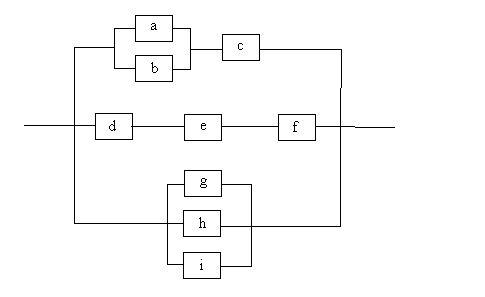
COMPLEX SERIES/PARALLEL SYSTEM RELIABILITY Many systems are seldom purely series or parallel combinations of components, but are mixtures of series and parallel components connected in series or parallel. The figure below shows such a system.

The reliability for the complex system shown above can be calculated by identifying the portions of the system that are purely series or parallel combinations and by replacing them with a single component whose reliability is equivalent to the combination. This process is repeated until the complex system is reduced to a single component. The calculated reliability of this component is the reliability of the system. In the above example, components a and b can be combined in parallel using

Rab = 1 - (1 - ra) * (1 - rb)

d, e and f can be combined in series

Rdef = rd * re * rf

components g, h and i can be combined in parallel.

Rghi = 1 - (1 - rg) * (1 - rh) * (1 - ri)

These combinations are replaced by a single component whose reliability is equal to the reliability of the combination.

A Partially Reduced Complex System

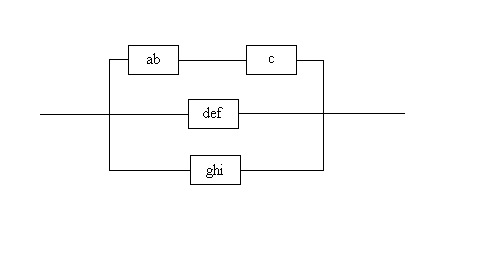
Next, the previously combined component ab can be combined with component c in series producing the network below.

A Partially Reduced Complex System

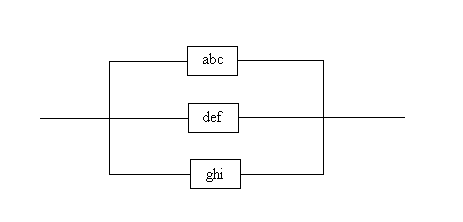
Finally, the reduced components abc, def and ghi can be combined in parallel to produce a single component (abcdefghi) whose reliability is equal to the reliability of the original complex system. In the complex system example above, let us assume the reliabilities of components a, c, f and i are .9, the reliabilities of components b and h are .95, the reliabilities of components d and g are .85 and the reliability of component e is .8. Following along with the system series/parallel reduction techniques outlined above, the parallel combination of components a and b (new component ab) has a reliability of .995; the series combination of components d, e and f (def) has a reliability of .612 and the parallel combination of components g, h and i result in a component (ghi) whose reliability is .99925. Next, combining ab with c in series gives a reliability of .8955 for new component abc. Finally, combining the previously reduced component abc, def and ghi in parallel gives a system reliability of .99997. Note that the order that we apply the series and parallel combination rules does not matter as long as the combinations are legitimate.  For example, if in Figure 8.8 we elect to combine components def and ghi in parallel and then combine components ab and c in series we would get the reduced network shown in the figure below. 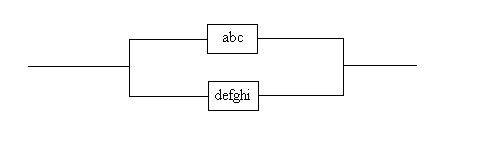A Partially Reduced Complex System In this reduced network. component abc has a reliability of .8955 as before and component defghi has a reliability of .997015.   When these two components are combined in parallel the total system reliability is the same as before:   .99997. 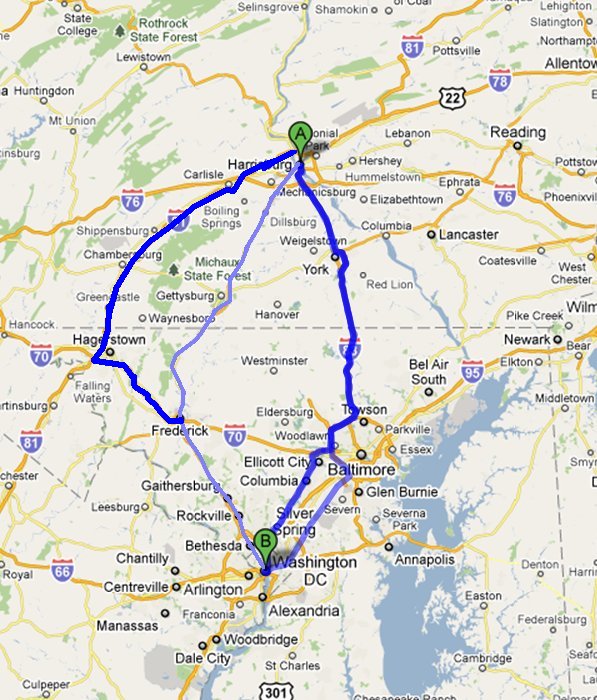The figure below gives a complex system example problem for the evacuation from Washington, DC to Harrisburg, PA.

A Routing Complex System

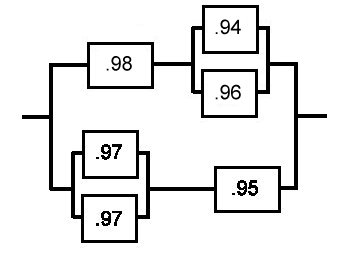
The reliability network schematic for this example is:

A Routing Complex System

The System Reliability is  .823372 The experienced emergency analyst can get a good idea of the reliability of a system such as this one without going through laborious calculations by applying the series heuristics and the parallel heuristics.  By applying the second series heuristic to the entire system, we see that the reliability of this system must be less than .85 since this first component of the system is in series with the rest of the system.   To estimate the true system reliability we need to investigate the rest of the system.  To make this process clear, we will proceed through the analysis in steps. The top three components are in series (reliabilities of .9, .8 and .95), so their combined reliability must be less than the lowest reliability component which is .8 using the series heuristic.  We will estimate this combined series reliability to be .7.   Next, we can estimate the reliability of the bottom two components (.88 and .9 reliabilities) in series to be approximately .8.   This combined component from step 2 is in parallel with the center component whose reliability is .9.  Their combined reliability must be greater than the larger of the two.   We will estimate this reliability at .95.  The left two components (.8 and .6 reliabilities) are in parallel.  We estimate their combined reliability to be .9.  This combined component from step 4 is in series with the previously combined component from step 3 (estimated reliability .95).  We will estimate the series reliability for the combination at .9.   This combined component (step 5) is in parallel with the upper three components that we previously estimated (step 1) to have a reliability of .7.  The parallel combination is estimated to have a reliability of .95. The combined component from step 6 represents the rest of the system and is in series with the component whose reliability is .85. The series combination must have a reliability less than the least reliable component, so we estimate the series reliability for this combination and thus the entire system at .8 Techniques such as this give the network designer a quick way to fairly closely estimate the reliability of complex systems without having to rely on time consuming mathematical calculations.  In the example shown above, the system reliability was estimated using heuristic techniques to be .8.  The computer program example calculated that same system reliability to be .823372.

Non Series/Parallel Systems Systems can be constructed of components that are neither in series or parallel nor are reducible to series or parallel subsystems.  Perhaps the simplest example of this is the mesh network.  The figure below shows a simple four node mesh network. Example Mesh Network 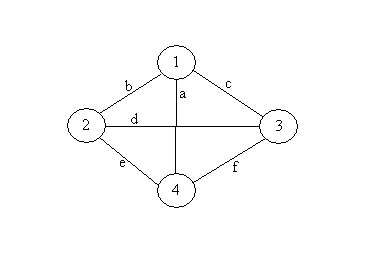A four mesh has six links which we have labeled a through f.  If we consider nodes 1 and 4 to be the terminal nodes (source and destination) for this network, then the network can be partitioned into two parallel subnetworks as shown in the figure below. Separated Four Node Mesh Network 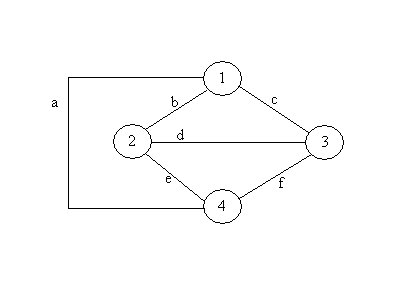The reliability of this mesh network can now be determined as the parallel combination of the a link and the remainder of the network, sometimes referred to as a bridge. Unfortunately, the remainder of the bridge network cannot be further defined in terms of serial and parallel components.   Therefore we must calculate its reliability from basic principles.  If we examine this bridge network, we can see that if all of the components are working the system will work with a probability of r5, where r is the component link reliability.  For simplicity in this derivation we have assumed all component reliabilities to be equal.   The reader can easily expand the derivation to include those instances where component reliabilities are different. If only one of the components has failed, the network system will still operate. The probability of one failure is r4(1-r) for each of the five cases in which ther is only one failure.   Similarly if any two components fail, the network system is still operable.  There are ten combinations where two components are failed and each has a probability of r3(1-r)2. The situation where three components have failed is a little more complex.  For three failed components, there are ten combinations of component failures.   The table below shows the states for the bridge network where three of the components have failed.  W is used to indicate that the component is working and F is used to indicate that the component has failed.  O is used to show that the system is operating and N is used where the system is not operating. Complex System Three Failure States     Link     Probability System b c d e f W W F F F r2(1-r)3 N W F W F F r2(1-r)3 N W F F W F r2(1-r)3 O W F F F W r2(1-r)3 N F W W F F r2(1-r)3 N F W F W F r2(1-r)3 N F W F F W r2(1-r)3 O F F W W F r2(1-r)3 N F F W F W r2(1-r)3 N F F F W W r2(1-r)3 N

Only two of the states where two components are operating contribute to the reliability of the network system.

Their probabilities are r2(1-r)3 each.  None of the states where four or five of the components have failed result in the network operating and thus do not contribute to reliability.  The reliability of the bridge network is therefore:

r5 + 5r4(1-r) + 8r3(1-r)2+2r2(1-r)3

This reliability in parallel with link a's reliability is the reliability for the mesh network.  The reliability of complex networks that are not decomposable into pure series or parallel components can be found in a similar manner.

Complex Example

Tesla Power Supply

The 85 kWh battery pack weighs 1,200 lb (540 kg) and contains 7,104 lithium-ion battery cells in 16 modules wired in series (14 in the flat section and two stacked on the front). Each module contains 6 groups of 74 cells wired in parallel.

The reliability of a module is:

rM = 1-( 1 - (rBattery)444.

The reliability of a battery pack is:

rP = rM16.

Panasonic 3.7v Protected Button Top Battery

Top View of Tesla Battery Assembly

Side View of Tesla Battery Assembly

Copyright © 2011 - 2020 Ken Sochats